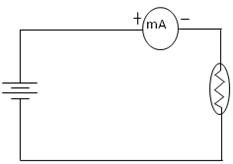
For Real Lab

• Connections are made as shown in the figure.

• Place the thermistor in an oil bath using the heating arrangement.

• Note the room temperature (T₀).

• Turn on the power supply and fix it to a constant voltage.

• Note the current readings using a digital multimeter or a milliammeter.

• Corresponding resistance is found using the equation:

• $R = \frac{V}{I}$ and is noted as R₀.

• Vary the temperature of the oil bath using the heating arrangement.

• Note the current readings at regular temperature intervals.

• Corresponding resistances R are found using the same equation.

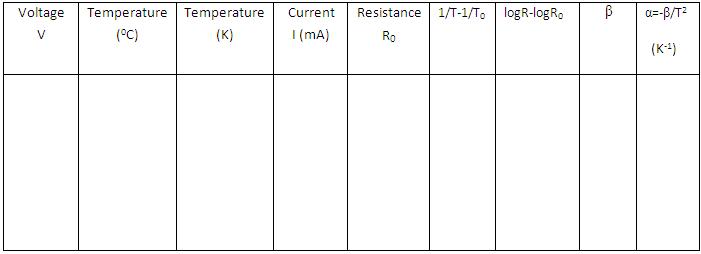
• From the readings, logR - logR₀ and 1/T - 1/T₀ are calculated.

• Value of β is calculated using the equation:
  

$\beta = \frac{\log R - \log R_0}{\frac{1}{T} - \frac{1}{T_0}}$

• Temperature coefficient of resistance is found using the equation: $\alpha = -\frac{\beta}{T^2}$

• Repeat the experiment for another voltage.

For Simulation

• Click on ‘Show Circuit Diagram’ to display the circuit.
• Place the mouse pointer over the components and click to drag wire.
• After connecting the components, click on the ‘Power On’ button in the variables region
• to start and maintain a constant voltage.

• Select the desired room temperature and choose any thermistor from the drop-down menu.
• The corresponding current reading is shown in the milliammeter.

• Resistance for that voltage value is calculated using the equation: $R = \frac{V}{I}$

• Increase the temperature using the slider shown in the variables region.
• Repeat the experiment for different voltage values and different thermistors.